Programs that write programs are the happiest programs in the world.

So, PL/SQL is kind of a weird language. There are things about it i don't like, and that's ok. There are two kinds of programming languages. The clean, elegant simple well designed languages, and the languages people actually use. So, I guess I make the world slightly uglier in a small corner no one will ever see, but my users are much much happier. So, PL/SQL it is.

Anyway, sometimes users set up a bunch of extra rows in constraint tables on production. For example, you might sell in 25 states, but only a few states are set up in the development database. If you're lucky and you have DBLinks set up, you can take advantage of the mighty left outer join. The idea is, you can look up what's missing on development.

The query looks something like this.

SELECT * FROM TableA
LEFT OUTER JOIN TableB
ON TableA.name = TableB.name
WHERE TableB.id IS null

Take a look at this coding horror to get a sense of what i'm talking about.

If we're clever, we can actually just look at the system tables to decide what the primary keys are for a given table, making it far easier to figure out how to compare the two tables. Here we're a little tricky, looking up the keys and then returning a list of column names. I think it's worth spending some time to learn all of the "as table" keywords. Those data structures come in handy all the time.

/* given a table name, return a list of column names that make up the primary key */
   FUNCTION f_constraint_query (v_target_table VARCHAR2)
      RETURN t_values
   IS
      v_query         VARCHAR2 (4000);
      v_constraints   t_values;
   BEGIN
      v_query :=
            'SELECT '
         || 'cols.column_name '
         || 'FROM all_constraints cons, all_cons_columns cols '
         || 'WHERE cols.table_name = '''
         || v_target_table
         || ''' AND cons.constraint_type = ''P'''
         || ' AND cons.constraint_name = cols.constraint_name'
         || ' AND cons.owner = cols.owner';

      EXECUTE IMMEDIATE v_query BULK COLLECT INTO v_constraints;

      RETURN v_constraints;
   END;

Depending on your environment, you could just do the insert's directly. I'm not in that sort of environment, so i just assemble the select statement to pull the data back to development. You should be able to just wrap the select in an insert into v_target_table, run EXECUTE IMMEDIATE and call it a day.

A coworker suggested chasing the foreign key references and recursively inserting everything as we go. I think that's a fantastic idea. It's just a slight mod to the above query. The problem is, our process just isn't clean enough yet. It'll get there.

   FUNCTION f_sel_prod_differences (v_target_table VARCHAR2)
      RETURN VARCHAR2
   IS
      v_query         VARCHAR2 (4000);
      v_constraints   t_values;
   BEGIN
      v_constraints := f_constraint_query (v_target_table);

      IF v_constraints.COUNT = 0
      THEN
         RAISE no_primary_key;
      END IF;

      -- find the stuff on production that's missing on devl
      v_query :=
            'select * from '
         || v_target_table
         || '@production r left outer join '
         || v_target_table
         || ' l ';

      -- add the primary key constraints to the join

      FOR i IN 1 .. v_constraints.COUNT
      LOOP
         IF i = 1
         THEN
            v_query := v_query || ' on l.';
         ELSE
            v_query := v_query || ' and l.';
         END IF;

         v_query :=
            v_query || v_constraints (i) || ' = r.' || v_constraints (i);
      END LOOP;

      v_query := v_query || ' where ';

      -- add the primary key constraints to the null finding part of the where clause
      FOR i IN 1 .. v_constraints.COUNT
      LOOP
         IF i = 1
         THEN
            v_query := v_query || ' l.' || v_constraints (i) || ' is null';
         ELSE
            v_query := v_query || ' and l.' || v_constraints (i) || ' is null';
         END IF;
      END LOOP;

      v_query := v_query || ';';
      -- DBMS_OUTPUT.put_line (v_query);
      RETURN v_query;
   END;

You should be able to just drop the two above queries into some utility package. be sure to update @production to reflect your actual install.

Screenshots

Terrain is coming along nicely. The differentiation stuff lets me calculate the curvature of the terrain at a given point, so I can use more polygons where the ground is curvy, and less where it's flat.




The more I learn about graphics programming, the more I realize I'm doing this wrong. The cpu's job is to tell the video card what to do. I'm doing all this clever dynamic level of detail stuff with terrain generated at run time, where I ought to just use a big file with all the polygons. Oh well, this way is pretty fun. If it is a performance problem i can always generate this stuff up front.

Higher order multivariate automatic differentiation in Haskell.

I've started a game in Haskell. I've run into a couple of situations where I need derivatives of multivariate equations. It's embarrassing how long i stared at this, Overloading Haskell numbers, part 2, Forward Automatic Differentiation. and this Non-standard analysis, automatic differentiation, Haskell, and other stories. without understanding what was going on. Finally I broke down and read this Lazy Multivariate Higher-Order Forward-Mode AD and this Lazy Differential Algebra and its Applications and the different approaches started to sink in. Like a first order level of understanding. I had a discussion with a physicist at work who kept looking at me like i had a second head when I was trying to explain the system. We talked through it, and finally things started to crystalize.

Looking back, as far as code changes go, this is trivial. Just substitute a set for a list, and provide indexed variables. Conceptually however, differentiation became very reminiscent of compilation. All my false starts at building up the sets of values remedied me of writing code for instruction selection. evaluating f(x) was similar to traversing an AST where actually building the sets for the derivatives was like code generation based on the AST. Blah blah blah, Math is hard, let's go shopping.

> module Diff where
> import qualified Data.IntMap as IM
> data Diff a = C a 
>             | D a (IM.IntMap (Diff a))
>               deriving (Eq,Ord,Show)

I keep track of the different known variables in an intmap. Following after Karczmarczuk, I use crappy names. C is for Constant. D is for Differentiable expression. Every Diff has a value, Differentiable expressions have a map of variable id's to differentiable expressions.

> dVar x id = D x $ IM.fromList [(id,C 1)]

for example, with a simple variable like dVar 3 0 this build the structure for variable id 0. The first derivative with respect to id 0 is 1, with respect to anything else, 0

> instance Functor Diff where
>     fmap f (C a) = C (f a)
>     fmap f (D a set) = D (f a) (IM.map (fmap f) set)

Although I don't use fmap as often as i should, Karczmarczuk's code used it. It's such a good idea. I have a nagging suspicion that i should implement map and fold for random datatypes i implement, then i never get around to doing it. If nothing else, it gives a nice understanding of how to really use the thing.

> add (C x) (C y) = C (x + y)
> add (C x) (D y vars) = D (x+y) vars
> add (D x vars) (C y) = D (x+y) vars
> add (D x vx) (D y vy) = D (x+y) (IM.unionWith (+) vx vy)

Add is great. Anything involving a constant is trivial. anytime there's a variable collision, add the children. So clean, so simple. So, (dVar 1 0) + (dVar 1 0) yeilds D 2 (fromList [(0,C 2)]). f(x) = x + x evaluated at 1 is 2(x), the first derivative makes the single variable fall away, giving just 2.

> mul (C x) (C y) = C (x * y)
> mul (C x) v = fmap (x*) v
> mul v (C y) = fmap (*y) v
> mul p@(D x vx) q@(D y vy) = D (x*y) (IM.unions 
>        [(IM.intersectionWith (\a b-> a * q + p * b) vx vy),
>         (IM.map (* q) (IM.difference vx vy)),
>         (IM.map (p *) (IM.difference vy vx))
>        ])

Mul took me a long time to get right. There's three cases to get just right. First, all of the overlapping derivatives must use the product rule. This is straight out of the list implementation. It wasn't at all obvious, to me, that the other cases are just multiplication. An afternoon with pencil an paper convinced me.

> df [] (C x) = Just x
> df [] (D x vars) = Just x
> df (i:is) (D x vars) = df is =<< (IM.lookup i vars)

df allows indexing into the resulting Diff structure. Nothing implies zero.

> test x y = x^3 * y + x^2 * y^2
> testdx x y = 3*x^2 * y + 2*x * y^2
> testdy x y = x^3 + x^2 * 2 * y
> testdx2 x y = 6*x * y + 2*y^2
> testdx2dy x y = 6*x + 4*y

Finaly some evaluations at 2 3.

*Diff> test 2 3
60
*Diff> df [] $ test (dVar 2 0) (dVar 3 1)
Just 60
*Diff> testdx 2 3
72
*Diff> df [0] $ test (dVar 2 0) (dVar 3 1)
Just 72
*Diff> testdy 2 3
32
*Diff> df [1] $ test (dVar 2 0) (dVar 3 1)
Just 32
-- here you can see the order of taking the derivitive dosn't matter. 
*Diff> testdx2dy 2 3
24
*Diff> df [0,0,1] $ test (dVar 2 0) (dVar 3 1)
Just 24
*Diff> df [1,0,0] $ test (dVar 2 0) (dVar 3 1)
Just 24
*Diff> df [0,1,0] $ test (dVar 2 0) (dVar 3 1)
Just 24

Everything else is cribbed from people much smarter than me. As i said before, substituting a map of variables to their respective derivatives is the only change through the rest of the code. See the links at the beginning of this article for beautiful derivations of the following.

> instance (Num a) => Num (Diff a) where
>     (+) = add
>     (*)= mul
>     negate = fmap negate
>     signum (C x) = C $ signum x 
>     signum (D x _) = C $ signum x
>     abs (C x) = C $ abs x
>     abs p@(D x _) = f $ fmap (*(signum x)) p
>         where f (D _ flip) = D (abs x) flip
>     fromInteger x = C (fromInteger x)

> instance (Fractional a) => Fractional (Diff a) where
>     recip (C x) = C (recip x)
>     recip (D x vars) = D (recip x) (IM.map (* (C (recip x * recip x))) vars)
>     fromRational r = C (fromRational r)

> lift (f:f') p@(D x vars) = D (f x) (IM.map (* lift f' p) vars)
> lift (f:f') p@(C x) = C (f x)

> instance (Floating a) => Floating (Diff a) where
>     pi = C pi
>     exp (C x) = C (exp x)
>     exp (D x vars) = r where r = D (exp x) (IM.map (mul r) vars)
>     log (C x) = C (log x)
>     log p@(D x vars) = D (log x) (IM.map (*(recip p)) vars)
>     sqrt (C x) = C (sqrt x)
>     sqrt (D x vars) = r where r = D (sqrt x) (IM.map (* (recip (2*r))) vars)
>     sin = lift (cycle [sin, cos, negate.sin, negate.cos])
>     cos = lift (cycle [cos, negate.sin, negate.cos, sin])
>     acos (C x) = C (acos x)
>     acos p@(D x vars) = D (acos x) (IM.map (* (negate $recip $sqrt $1-p*p)) vars)
>     asin (C x) = C (asin x)
>     asin p@(D x vars) = D (asin x) (IM.map (* (recip $sqrt $1-p*p)) vars)
>     atan (C x) = C (atan x)
>     atan p@(D x vars) = D (atan x) (IM.map (* (recip $ p*p+1)) vars)
>     sinh x = (exp x - exp (-x))/2
>     cosh x = (exp x + exp (-x))/2
>     asinh x = log (x + sqrt (x*x + 1))
>     acosh x = log (x + sqrt (x*x - 1))
>     atanh x = (log (1+x) - log(1-x))/2

Oh, by the way, this post, like the others is literate haskell, just paste it into a text file with a .lhs suffix and you can run it all.

Jason

-- edit -- added negate to the Num instance, as turingtest suggested. Thanks.
-- edit -- flipped sine in atan as luis suggested.

OpenGL programming with Haskell

I've spent the last few weekends playing with Haskell OpenGL programming. It's pretty awesome. I've begun to see the design of larger haskell programs as a thin imperative shell around a pure functional core. At first, I followed along with everyone else, doing everything in the IO monad, but there is a better way. Two key insights led me to this shell style program.

First, i realized game state really had to live in an IO ref. That made me sad, so i took up a policy of containment. The OpenGL windowing system works on callbacks. you have to specify the functions that will actually handle keystrokes, but they don't have to do any work. I guess an example is in order:

> {-# OPTIONS -fglasgow-exts #-}
> import Data.IORef
> import qualified Graphics.UI.GLUT as GL
> import System.Exit

Three things to take care of. 1. Initialize OpenGL. 2. Create the game world. 3. Set up the callbacks. The window Utilities actually enter into a main loop that keeps track of all the openGL gunk. when it's time to render a new frame, the Display callback is responsible for sending commands to the GL device. The idle callback tells us how to update the world as time passes. The keyboardMouseCallback is, shockingly, called when the user clicks the mouse, moves the mouse, or types.

> main = do
>  (progname, _) <- GL.getArgsAndInitialize
>  window <- initGL
>  gameEnv <- newIORef initialWorld
>  GL.displayCallback $= (display gameEnv)
>  GL.idleCallback $= Just (idle gameEnv)
>  GL.keyboardMouseCallback $= Just (keyboardMouse window gameEnv)
>  GL.mainLoop

The initGL method is at the end, because it's boring. It's just what you'd expect to see in any random openGL tutorial. The callbacks are here, because they're slightly more interesting. Notice how they pass *all* the work off to helper methods.

Display gets the current game state, and asks render to render it.

> display gameEnv = do
>  GL.clear [GL.ColorBuffer , GL.DepthBuffer]
>  env <- GL.get gameEnv
>  render $ world env
>  GL.swapBuffers

The idle method keeps track of how much time is passing. time and game state gets passed on to tick.

> idle gameEnv = do
>  env <- GL.get gameEnv
>  time <- GL.get GL.elapsedTime
>  gameEnv $= tick time env
>  GL.postRedisplay Nothing

Finally input handling. Virtually the same as idle, grab the state change, and pass it on to the pure handler.

> keyboardMouse window _ (GL.Char '\ESC') GL.Down _ _ = do
>   GL.destroyWindow window
>   exitWith ExitSuccess
> keyboardMouse _ gameEnv key state modifiers position = do
>  env <- GL.get gameEnv
>  gameEnv $= userAction env key state

Now we've got our callbacks... what do they actually do?
Time for some datatypes

> type Time = Int
> data GameEnv = GameEnv Time User
>                deriving Show
> data User = User { playerX :: GL.GLfloat,
>                    playerY :: GL.GLfloat,
>                    playerVelocityX :: GL.GLfloat,
>                    playerVelocityY :: GL.GLfloat,
>                    playerRotation :: GL.GLfloat,
>                    playerVelocityRotation :: GL.GLfloat
>                  }
>           deriving Show
>
> initialWorld = GameEnv 0 $ User 0 0 0 0 0 0

Our game environment is simply a clock, and some bookkeeping state about the user's position and velocity. Obviously, store whatever you need to here. If bad guys should chase the user, this is where you store their state. This example renders the world based on time, to keep things simple.

The idle timer calls tick once for each pass through the mainloop. This reflects time passing in the world. If you have bad guys, move them here. Two things are going on, and perhaps it's a little confusing. First the elapsed time is calculated, and stored in the new game environment. Second, the player's position is updated based on their current velocity in the x, and y dimensions. The rotation is updated based on the angular velocity.

> tick :: Int -> GameEnv -> GameEnv
> tick tnew (GameEnv 0 usr) = GameEnv tnew usr
> tick tnew (GameEnv told usr) = GameEnv tnew u
>     where u = usr{playerX = (playerVelocityX usr)/100 * elapsed + (playerX usr), 
>                   playerY = (playerVelocityY usr)/100 * elapsed + (playerY usr),
>                   playerRotation = (playerVelocityRotation usr)/100 * elapsed + (playerRotation usr)}
>           elapsed = fromIntegral $ tnew - told

Next, player actions. I think these are ugly because of their verbosity. and there's lots of them. However, they are very simple. I simply set the velocity. a nicer approach would set acceleration, and cap the maximum velocity. That lets you ease in and ease out of motion, but that code gets fairly opaque.

Arrow up, moves the player forward, arrow down moves back.

> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyUp) GL.Down = GameEnv t u
>    where u = usr{playerVelocityX = sin $ pi / 180 * playerRotation usr,
>                  playerVelocityY = 0 - (cos $ pi / 180 * playerRotation usr)}
> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyUp) GL.Up = GameEnv t u
>    where u = usr{playerVelocityX = 0, playerVelocityY = 0}

> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyDown) GL.Down = GameEnv t u
>    where u = usr{playerVelocityX = 0 - (sin $ pi / 180 * playerRotation usr),
>                  playerVelocityY = cos $ pi / 180 * playerRotation usr}
> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyDown) GL.Up = GameEnv t u
>    where u = usr{playerVelocityX = 0, playerVelocityY = 0}

Left and right, update the player rotation velocity.

> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyLeft) GL.Down = GameEnv t u
>    where u = usr{playerVelocityRotation = (-10)}
> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyLeft) GL.Up = GameEnv t u
>    where u = usr{playerVelocityRotation = 0}

> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyRight) GL.Down = GameEnv t u
>    where u = usr{playerVelocityRotation = 10}
> userAction (GameEnv t usr) (GL.SpecialKey GL.KeyRight) GL.Up = GameEnv t u
>    where u = usr{playerVelocityRotation = 0}

I considered the standard W A S D keys, but I wanted to figure out the special keys. I use Q W for strafe, so there is an example of side to side motion.

> userAction (GameEnv t usr) (GL.Char 'q') GL.Down = GameEnv t u
>    where u = usr{playerVelocityY = 0- (sin $ pi / 180 * playerRotation usr),
>                  playerVelocityX = 0- (cos $ pi / 180 * playerRotation usr)}
> userAction (GameEnv t usr) (GL.Char 'q') GL.Up = GameEnv t u
>    where u = usr{playerVelocityX = 0, playerVelocityY = 0}

> userAction (GameEnv t usr) (GL.Char 'w') GL.Down = GameEnv t u
>    where u = usr{playerVelocityY = (sin $ pi / 180 * playerRotation usr),
>                  playerVelocityX = (cos $ pi / 180 * playerRotation usr)}
> userAction (GameEnv t usr) (GL.Char 'w') GL.Up = GameEnv t u
>    where u = usr{playerVelocityX = 0, playerVelocityY = 0}

Anything else, ignore.

> userAction g _ _ = g

That pretty much covers my first insight, forcing state as high up as possible. Main, is in the IO monad. The callbacks are in the IO monad. Everything else is pure. Everything else is QuickCheck-able. The trick to rendering, I feel, is preserving purity. My solution is a dsl. Constructing the world is constructing a list of OpenGL commands for the renderer to execute.

Existential types seem to be the only way out. Existential types allow us to group things simply by functionality. So, many datatypes instance the same class. First and foremost, GLCommand. a glcommand has a render method, it executes in the IO monad. So, the intention is, we will render a list of renderable things.

> class GLCommand a where
>     render :: a -> IO ()

Next, the Existential type. This says anything that is a GLCommand, is also a GLC. a GLC is renderable. We get to make lists of GLC's, the only requirement is that each element is renderable, each element has a render method.

> data GLC = forall a. GLCommand a => GLC a
> instance GLCommand GLC where
>     render (GLC a) = render a

The wiki has a much more coherent explanation of existential types, check it out here: http://www.haskell.org/haskellwiki/Existential_type

There's a few fundamental operations I'd like to use to compose my scene. Matrix operations, vertex creation, colors. My approach creates a datatype that encapsulates everything the render method will need to generate the GL operation at render time. I have 4 basic matrix operations. All I do is wrap up the desired state in a datatype.

> rotate :: GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GLC
> rotate a v1 v2 v3 = GLC $ ActionRotate a (GL.Vector3 v1 v2 v3)
> scale :: GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GLC
> scale x y z = GLC $ ActionScale x y z
> translate :: GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GLC
> translate x y z = GLC $ ActionTranslate (GL.Vector3 x y z)
> identity = GLC $ (ActionIdentity :: MatrixActions GL.GLfloat)

The actual datatype is simple. Again, just hold the data that the GL methods will require at render time.

> data GL.MatrixComponent a => MatrixActions a = ActionRotate a (GL.Vector3 a)
>                                              | ActionScale a a a
>                                              | ActionTranslate (GL.Vector3 a)
>                                              | ActionIdentity 

Finally instancing the GLCommand class, The render method does the work of rotation, or scaling, or whatever is necessary. This style fully separates the IO stuff from rendering a scene.

> instance GL.MatrixComponent a => GLCommand (MatrixActions a) where
>     render = matrixActions
> matrixActions (ActionRotate angle vec) = GL.rotate angle vec
> matrixActions (ActionScale x y z) = GL.scale x y z
> matrixActions (ActionTranslate vec) = GL.translate vec
> matrixActions (ActionIdentity) = GL.loadIdentity 

Vertex creation, and setting colors follow a similar pattern.

> data GL.VertexComponent a => VertexActions a = ActionVertex (GL.Vertex3 a)
> instance GL.VertexComponent a => GLCommand (VertexActions a) where
>     render = vertexActions
> vertexActions (ActionVertex vec) = GL.vertex vec
> vertex :: GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GLC
> vertex x y z = GLC $ ActionVertex (GL.Vertex3 x y z)
> data GL.ColorComponent a => ColorActions a = ActionColor (GL.Color3 a)
> instance GL.ColorComponent a => GLCommand (ColorActions a) where
>     render = colorActions
> colorActions (ActionColor c) = GL.color c
> color :: GL.GLfloat -> GL.GLfloat -> GL.GLfloat -> GLC
> color r g b = GLC $ ActionColor (GL.Color3 r g b)

The final operations were inspired by http://www.cs.unm.edu/~williams/cs257/graphics.html The idea is when rendering sometimes we want to draw things one after the other, in series. However, sometimes we want to draw a little bit, then go back, and draw a bit more. An example might be drawing the branches of the tree. After drawing the trunk, draw one branch away from the trunk, then jump back to the trunk and draw another branch.

So here are the basic operations:

> triangles commands = GLC $ RenderTriangles commands
> serial commands = GLC $ RenderSerial commands
> parallel commands = GLC $ RenderParallel commands

Now, rather than simple operations I gather lists of operations.

> data RenderActions = RenderTriangles [GLC]
>                    | RenderSerial [GLC]
>                    | RenderParallel [GLC]
> instance GLCommand RenderActions where
>     render = renderActions
> renderActions (RenderTriangles commands) = GL.renderPrimitive GL.Triangles $ mapM_ render commands
> renderActions (RenderSerial commands) = mapM_ render commands
> renderActions (RenderParallel commands) = mapM_ (GL.preservingMatrix . render) commands

The world itself. World's job is to take the current game environment, then come up with a list of commands to execute to render that world.

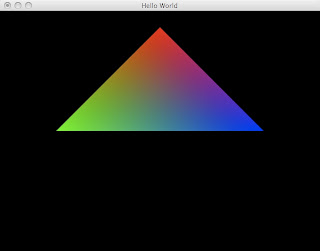
> world (GameEnv t u) = serial [ identity,
>                                rotate (playerRotation u) 0 1 0,
>                                translate (0 - playerX u) 0 (0 - playerY u),
>                                translate 0 0 (-4),
>                                rotate trotation 0 1 0,
>                                triangles [ color 1 0 0,
>                                            vertex 0 1 0,
>                                            color 0 1 0,
>                                            vertex (-1) 0 0,
>                                            color 0 0 1,
>                                            vertex 1 0 0]]
>                       where trotation = (fromIntegral t) / 10

This is some random housekeeping stuff, initialization of GL and a few commands to clean up the syntax a bit.

> ($=) :: (GL.HasSetter s) => s a -> a -> IO ()
> ($=) = (GL.$=)

> initGL = do
>  GL.initialDisplayMode $= [GL.DoubleBuffered]
>  GL.initialWindowSize $= GL.Size 640 480
>  GL.initialWindowPosition $= GL.Position 0 0
>  window <- GL.createWindow "Hello World"
>  GL.clearColor $= GL.Color4 0 0 0 0
>  GL.viewport $= (GL.Position 0 0 , GL.Size 640 480)
>  GL.matrixMode $= GL.Projection
>  GL.loadIdentity
>  GL.perspective 45 ((fromIntegral 640)/(fromIntegral 480)) 0.1 100
>  GL.matrixMode $= GL.Modelview 0
>  return window

It would be great to expand the existential types to only allow the setting of vertexes in a triangle command. I haven't gotten around to that in my toy programs.

There you go. A complete system for developing large opengl applications in a few hundred lines of code.

Association trees

I'm sure someone has done this before, but i haven't seen it. Originally developed in scheme, this implementation is for lisp. It ought be jazzed up with support for keywords.

The idea is, rather than a simple assoc list,

((a . 1) (b . 2) (c . 3))

use a full tree representation, where the children may be association lists themselves. Like this:

(tree-assoc '(a b c) ((a (b (c . 1) (d . 2))))) -> (c . 1)


The implementation is simple, just recur until the path runs out.

(defun tree-assoc (path tree)
  (cond
    ((null path) ())
    ((null (cdr path)) (assoc (car path) tree))
    (t (let ((subtree (assoc (car path) tree)))
  (and subtree (tree-assoc (cdr path) (cdr subtree)))))))

The original motivation came from a DnD character builder. I was running into trouble, because i wanted to use the key 'bonus far to often. The tree structure lets me segregate keys, so i can use duplicate keys. The real power became apparent when i wrote tree-insert. This gives a nice, simple, queryable representation of hierarchical data.

(defun tree-insert (path tree item)
  (cond
    ((null path) item)
    ((not tree) (build-path path item))
    (t (let ((node (assoc (car path) tree)))
  (acons (car path)
  (if node
      (tree-insert (cdr path) (cdr node) item)
      (build-path (cdr path) item))
  (remove (car path) tree :key #'car))))))

(defun build-path (path item)
  (if (null path) 
      item
      (acons (car path) (build-path (cdr path) item) ())))

Solitaire

I was getting mighty sick of socket programming, so I did what any good programmer does. Procrastinate by surfing the web. I happened upon haskell.org's collection of solutions to the Ruby quiz puzzles, in Haskell. The random page function is neato. I took a stab at the first one, Bruce Schneier's solitaire cypher.

I spent a lot of time reading up on list manipulation functions in Data.List. That library is awesome. I didn't really grok the utility of zipWith until I caught myself thinking, I have two lists i would like to combine. Another function I put to good use was groupBy. groupBy is sort of odd, but i think there's a fair amount of utility there. I couldn't' think of a clever way to break a list up into a list of lists of 5 elements. it's *almost* like map, but needs to look at more of the list. I suppose there's something like reverse $ foldl (\acc val -> if (length head acc < 5) then (val:(head acc)):(tail acc) else [val]:acc but that seems opaque.

I ran into a couple of problems, I need to learn to read specifications very carefully. I wasted a fair amount of time by missing the part that both Jokers are considered 53 when used in a numeric context, I had used one Joker as 53 and another as 54. There were also some fiddly little details with converting from numeric to ascii codes... off by one error essentially.

Anyway, check out the quizzes. they're nice sized problems. Challenging enough to be more than a toy, but not so large that they're daunting. Keep a window on the haskell libraries open too. There's great stuff in the library you'll never realize you need till you're in the thick of a problem. Well, it worked well for me anyway.

Simple Socket Programming 2. Revenge of the chat.

See Part 1.

Chat is a much more interesting server application than webserver. Each thread of control must communicate with every other thread. Or, at least, with some sort of authority that communicates with every other thread.

I'm going to be explicit about where declarations come from. It's a lot easier to sort out where to look for documentation with this style of import.

> import Control.Concurrent (forkIO)
> import Control.Concurrent.STM (STM, TVar, atomically, newTVar, readTVar, writeTVar)
> import Control.Exception (bracket, finally)
> import Network (PortID(..), accept, sClose, listenOn)
> import System.IO (Handle, hClose, hFlush, hGetLine, hPutStrLn)

There are a whole different set of problems to solve when clients can talk to each other. The original threaded server simply used the bracket function to take care of all of the looping. Chat requires each thread to have access to every other thread.

> threaded  talk = 
>     do { state <- atomically (newTVar [])
>        ; bracket (listenOn $ PortNumber 8000) 
>                      (sClose) 
>                      (loop state) }
>     where loop s sock = do { c <- accept sock  
>                            ; threadCreator s talk c
>                            ; loop s sock}

Three changes, First the creation of state. This state var is passed down to each client thread. This is the key to interprocess communication. Every thread can read and write this variable, so they have a way to talk to each other. The second big change is simplifying the where clause. loop is a little bigger than I'm comfortable with, but i think the code is clear. handle was pulled out, and promoted to a top-level function, threadCreator. Third, the protocol was removed from the server. Threaded and threadCreator only concern themeelves with socket level interaction. Protocol for using the sockets is dealt with by whatever talk function is passed in.

> threadCreator state talk (h, n, p) = 
>     do { manipState state (\x -> h:x) 
>        ; forkIO $ finally (talk h state)
>                     (do { manipState state
>                           (\x -> filter (h /=) x)
>                         ; hClose h})}

ThreadCreator has a lot more work to do. When threaded accepts a connection threadCreator puts that connection into the global state. Conceptually, when we get a connection, cons it on to the list of all the connections. Then, when we're done talking to a client threadCreator removes the closed handle from the list of connections. manipState does the work of adding and removing the connections from the list.

ThreadCreator got some complexity from exception handling. before, a thread could lose it's socket and just die. Now we have special resources that must be cleaned up. ThreadCreator has one wonderful property that i feel more than makes up for it's clumsiness. ThreadCreator cleans up all of the resources it creates with no special handling. Everything you ever need to know about manipulating the global state is right there. All of the side effects are locked down to six lines of code. Anyone who's some time chasing malloc/free or new/delete pairs will appreciate how important this really is.

> manipState state op = 
>     atomically $ do { ls <- readTVar state
>                     ; writeTVar state $ op ls}

ManipState is a simple helper. perhaps it should go in a where block of threadCreator, but I'm wary of extensive where blocks. The point is, given some state, read the state, operate on it then write the state back.

> tell h s = hPutStrLn h s >> hFlush h
> echo h s = tell h "echo!" >>
>            loop
>     where loop = hGetLine h >>= tell h >> loop

Here we have a simple echo talk protocol to verify everything compiles and appears to work. running threaded echo in ghci fires up the server. It appears to echo back whatever i type at it. It also appears well behaved on disconnect. The last step is to really chat, with threads talking to each other.

> tellAll h s = mapM (\x -> tell x s) h

> chat :: Handle -> TVar [Handle]->IO a
> chat h s = tell h "chat!" >>
> loop
> where loop = do { msg <- hGetLine h
> ; ls <- atomically(readTVar s)
> ; tellAll ls msg
> ; loop }

Try threaded chat from a ghci prompt, or main = threaded chat for ghc.

The chat client handler thread reads a message, then writes that message to every open handle. The one big problem with this approach is simultaneous messages. There's a race condition where to threads may write to the output handle at the same time. This could garble client 1's message "foo" and client 2's message "bar" resulting in something like "fboo" and "ar". More serious is the case where client 1 disconnects, just as client 2 is writing to the handle. client 2 will get an io exception and be disconnected.

These problems could be solved with more state, and more error checking. I'll address them in part 3. As a preview, haskell threads are so inexpensive i think a good solution would be one thread for reading every handle, and another thread for writing every handle. That approach needs more sophisticated shared state. The basic idea is each reader thread calls a dispatch function, much like talk. The dispater writes to one or more TChan channels. The writer threads take data from the tchan, and put it on the socket.

Jason